Beware the quadratic gas cost of memory allocation
Here we have a skeleton for an Auction contract. What do you think the gas cost of the
alreadyBid function is in terms of the number of bidders? Would it be O(n)?
contract Auction {
struct Bid {
uint256 amount;
address bidder;
}
Bid[] public bids;
function bid() external payable {
require(!alreadyBid(msg.sender), "Already submitted a bid!");
require(msg.value > 0, "Must bid non-zero amount!");
Bid memory newBid = Bid(msg.value, msg.sender);
bids.push(newBid);
}
function alreadyBid(address bidder) private view returns (bool) {
for (uint256 i = 0; i < bids.length; ++i) {
Bid memory bid = bids[i];
if (bid.bidder == bidder)
return true;
}
return false;
}
// Other auction functions down here...
}
If you’re not a seasoned Solidity engineer then it would be reasonable to think so… but lurking in Appendix H of the Ethereum yellow paper is a fact that’s easy to miss:
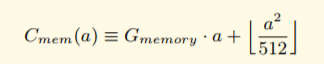
G_memory is fixed at 3 gas and is linear in the number of words the memory space has expanded to. But once the number of words exceeds 22 (a^2 > 512 => a > 22), it becomes quadratic, or O(n^2)!
Avoid unbounded for loops at all costs, especially when the operation that grows the number of
iterations is out of your control (like executing a public bid function that’s callable by
anyone).
Also, if you feel the need to use unbounded for loops then you might want to rethink your design. There’s often a way to do it better. We can avoid unbounded for loops in the auction contract by storing bids in a map instead of an array.
contract Auction {
struct Bid {
uint256 amount;
address bidder;
}
mapping(address => Bid) public bids;
function bid() external payable {
require(!alreadyBid(msg.sender), "Already submitted a bid!");
require(msg.value > 0, "Must bid non-zero amount!");
Bid memory newBid = Bid(msg.value, msg.sender);
bids[msg.sender] = newBid;
}
function alreadyBid(address bidder) private view returns (bool) {
return bids[bidder].amount > 0;
}
// Other auction functions down here...
}